

Rotating frame analysis is a specialized part of relative motion analysis. It is typically performed in Cartesian (\(x\)-\(y\)) coordinates for rigid bodies. In the previous section, rotating frames in polar coordinates were used to solve problems with formulae similar to those in particle kinematics. We will adopt a slightly different notation that is specialized to rigid bodies. These formulae are the most general planar kinematics formulae - that is, they can always be used, and will provide the correct answer. However, they are unnecessarily complicated for many types of motion, such as pure rotation. Rotating frame analysis is really important for cases where objects are not pinned to each other. When do you use rotating frames? When one object is sliding against another object, or two objects are not even in contact, but you want to know something about the motion relationship between them and/or are given information about the motion relationship between them.
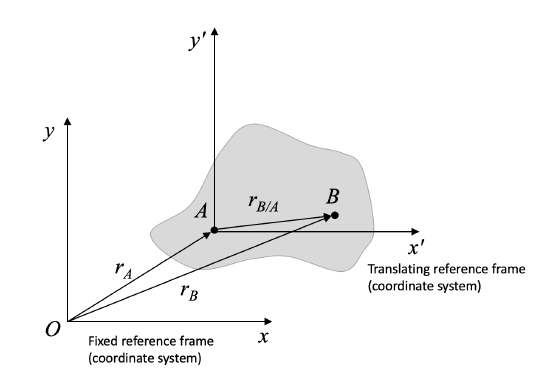
In most of the preceding material, you have worked with the fixed reference frame \(O_
Now, we will consider a reference frame that is attached to a point on the rigid body and both rotating and translating with the rigid body. We will introduce some extra terms to account for the rotation of the frame. Consider a rigid body with frame \(x'y'z'\) at point \(A\). \(x'y'z'\) moves and rotates with the body. A bug, \(B\), is crawling along the body. 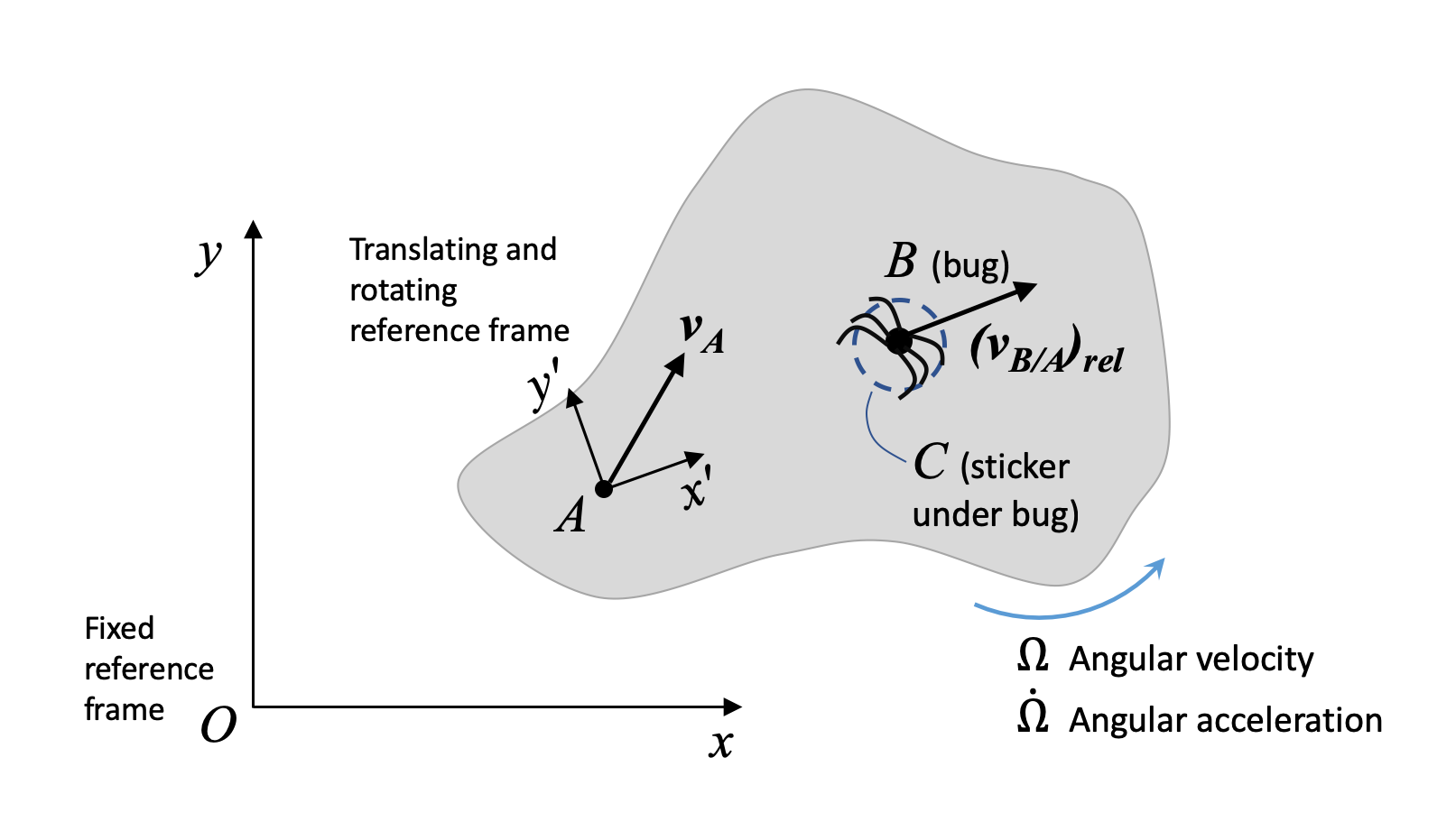 For an observer sitting at \(A\), the bug appears to be crawling away in a straight line. But for an observer sitting at \(O\), the bug does not look like it is moving in a straight line, because the body it is crawling on is also moving (translating and rotating). We would like to describe the motion of the bug as seen by an observer at \(O\). To remind ourselves that we are dealing with a rotating frame attached to one body, we use capital omega \(\Omega\)) to denote the angular velocity of the object that the rotating frame is attached to, and \(\dot<\Omega>\) for the angular acceleration of the object with the rotating frame attached. Finally, we use brackets and the subscript \(rel\) to denote values of velocity or acceleration expressed with respect to the rotating frame. Recall that vectors have both magnitude and direction. We can express a vector in components with respect to the \(\hat\) and \(\hat\) unit vectors: \[ \vec_ = r_ \hat + r_ \hat \] Normally, when we take a time derivative of such an expression, the length of the vector (i.e. the \(r_\) and \(r_\) terms) change, but the unit vectors do not. In the case of the rotating frame, the unit vectors change. Now, they don't change in length - they remain unit vectors. But they are attached to a rotating body, which means they also rotate. That is, their directions change, and we have to account for that when deriving velocity and acceleration expressions.
For an observer sitting at \(A\), the bug appears to be crawling away in a straight line. But for an observer sitting at \(O\), the bug does not look like it is moving in a straight line, because the body it is crawling on is also moving (translating and rotating). We would like to describe the motion of the bug as seen by an observer at \(O\). To remind ourselves that we are dealing with a rotating frame attached to one body, we use capital omega \(\Omega\)) to denote the angular velocity of the object that the rotating frame is attached to, and \(\dot<\Omega>\) for the angular acceleration of the object with the rotating frame attached. Finally, we use brackets and the subscript \(rel\) to denote values of velocity or acceleration expressed with respect to the rotating frame. Recall that vectors have both magnitude and direction. We can express a vector in components with respect to the \(\hat\) and \(\hat\) unit vectors: \[ \vec_ = r_ \hat + r_ \hat \] Normally, when we take a time derivative of such an expression, the length of the vector (i.e. the \(r_\) and \(r_\) terms) change, but the unit vectors do not. In the case of the rotating frame, the unit vectors change. Now, they don't change in length - they remain unit vectors. But they are attached to a rotating body, which means they also rotate. That is, their directions change, and we have to account for that when deriving velocity and acceleration expressions. 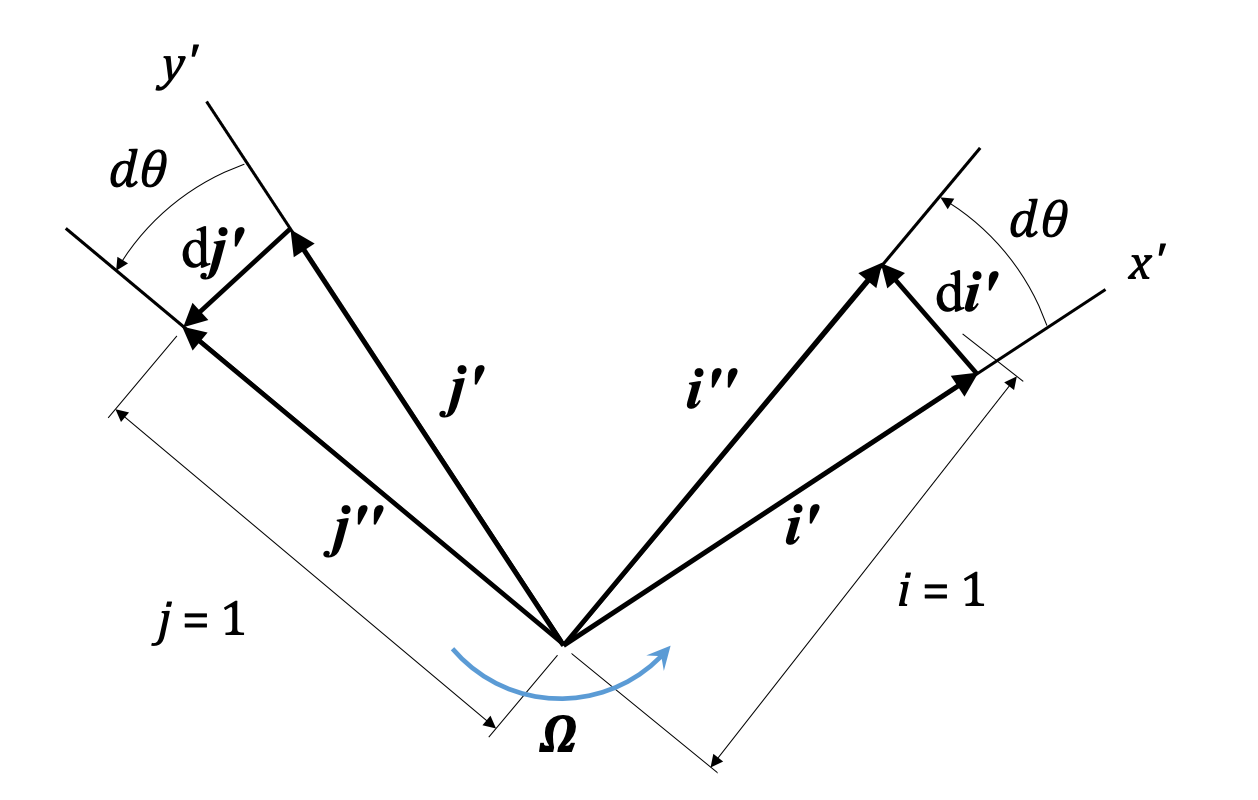 You can see we get small vectors \(d \hat\) and \(d \hat\) that describe the change in direction of the unit vectors, and the magnitude of that change is directly related to \(\Omega\), the angular velocity of the rigid body and the rotating frame. \[ \frac
You can see we get small vectors \(d \hat\) and \(d \hat\) that describe the change in direction of the unit vectors, and the magnitude of that change is directly related to \(\Omega\), the angular velocity of the rigid body and the rotating frame. \[ \frac
| Motion of rotating frame attached to rigid body: | \( \vec_ + \dot<\vec<\Omega>> \times \vec_ + \vec <\Omega>\times ( \vec <\Omega>\times \vec_ ) \) |
| Coriolis acceleration - interaction of object motion with respect to rotating frame and motion of rotating frame: | \( 2 \vec <\Omega>\times (\vec_)_ \) |
| Motion of object with respect to rotating frame: | \( ( \vec_ )_ \) |
These are some of the most complex problems in planar kinematics, so take your time!
A camera drone, \(D\), flies over a car race in a curved trajectory (center \(O\)) with a constant ground-speed velocity of \(v_D = 9 \ m/s\). At the moment shown, car \(C\) is traveling with velocity of \(v_c = 12 \ m/s\) and an acceleration of \(a_c = 2 \ m/s^2\) as shown. Assume \(d_1 = 7.5 \ m, \ d_2\) = \ 3 m\).
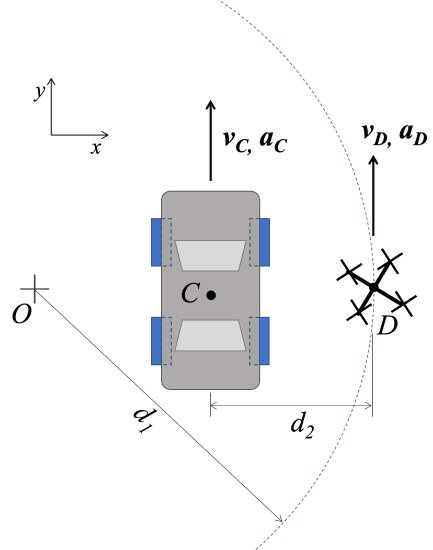 Solution
Solution Solution
Solution
Video \(\PageIndex<2>\): Worked solution to example problem \(\PageIndex<2>\), provided by Dr. Jacob Moore. YouTube source: https://youtu.be/mL0PVJNnOBE.
This page titled 11.5: Rotating Frame Analysis is shared under a CC BY-SA 4.0 license and was authored, remixed, and/or curated by Jacob Moore & Contributors (Mechanics Map) via source content that was edited to the style and standards of the LibreTexts platform.